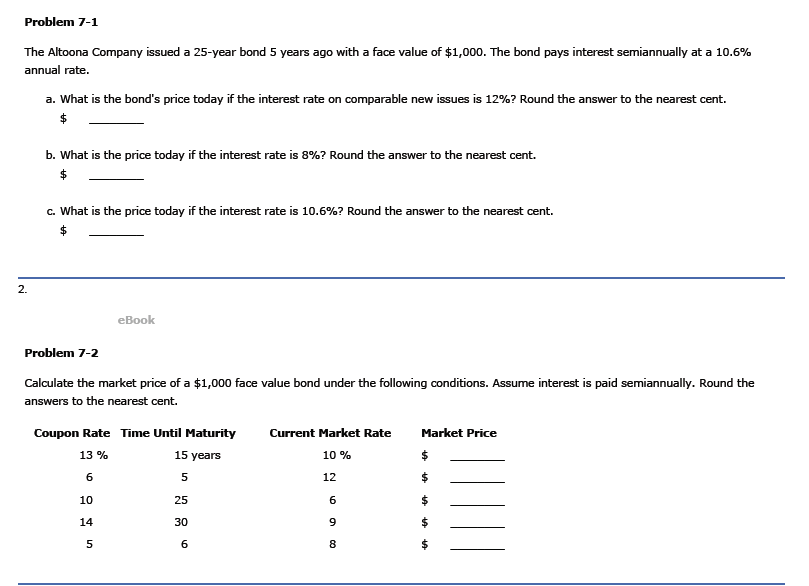
P= PMT [PVFAK,n] + FV [PVFK,n) ]
A
n = 20 *2
2 = 40k = 12/2 = 6
PMT = $1,000
.10.6/2 = $53
FV = $1,000
Pb= = $53 [PVFA6,40] + $1,000 [PVF6,40]
= $53 (15.0463) + $1,000 (.0972)
= $894.65
B
k = 8/2 = 4
= $53 [PVFA4,40] + $1,000 [PVF4,40]
= $53 (19.7928) + $1,000 (.2083)
= $1257.3184
C
c. In part a the interest rate has risen above the coupon rate. Therefore an investment equal to the bond’s face value would earn more if placed in newly issued bonds. That means the bond’s price has to decrease below face value to keep its yield competitive with new issues. In part b the bond offers more than new issues costing $1,000. Therefore, its price can increase above $1,000 and still remain competitive.
A
PB = PMT [PVFAK.n ] + FV [PVFk.n)
65 [PVFA5,30] + $1,000 [PVF5,30]
= $65 (15.3725) + $1,000 (.2314)
= $1230.6125
B
.PB= $30 [PVFA6,10] + $1,000 [PVF6,10]
= $30 (7.3601) + $1,000 (.5584)
= $779.203.
C
PB= $50 [PVFA3,50] + $1,000 [PVF3,50]
= $50 (25.7298) + $1,000 (.2281)
= $1,514.59
D
.PB= $70 [PVFA4.5,60] + $1,000 [PVF4.5,60]
= $70 (20.638) + $1,000 (.0713)
== $1,515.96
E
PB= $1,515.964,12] + $1,000 [PVF4,12]
= $25 (9.3851) + $1,000 (.6246)
= $859.23